ODG

光設計賞

光設計特別賞

奇数次非球面の数学的基礎の解明と光学設計への応用

　　　受賞者　：田邉　貴大

　　　所属　　：昭和オプトロニクス株式会社

左から審査委員長の辰野氏、受賞者の田邉氏

授賞理由

　奇数次非球面に関し、光学設計面の基本的な理論をしっかり整理した点と、Zernike多項式の数学的な意味を明確にしたことで、製造/計測における解析の基礎を強固にした点を評価します。奇数次非球面の有効性を理論的に示したことは、今後の光学設計開発に繋がる重要な成果であり、光設計特別賞を授与します。

概要

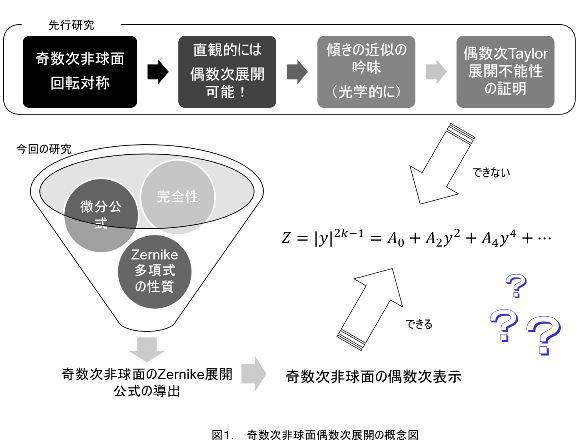
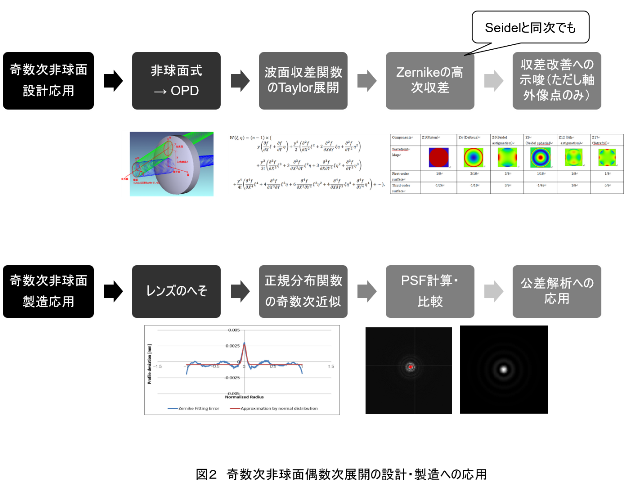
　従来、奇数次非球面は光学設計に用いられてきたが、その理論的背景は明らかではなかった。特に偶数時非球面による近似の収束性、および傾きの近似の完全性と収束性の議論は不完全なものであった。また、奇数次非球面の収差設計への有効性の理論的検討も不十分であった。
　本研究ではまず、奇数次非球面のZernike展開における傾きまで含めた完全性と収束性を初めて示した。これを有限項で打ち切ることにより、奇数次非球面の偶数次非球面による傾きまで含めた近似可能性を導いた。次に波面展開による奇数次非球面の収差係数を独自の手法で導出した。実例としてEUVL投影光学系の設計に応用し、奇数次非球面の収差特性が設計に有効であることを明らかにした。さらに、奇数次非球面の製造面への応用としてレンズのへそ（非球面加工痕）の近似に有効であることを実証した。一連の研究により、奇数次非球面の数学的基礎を確かにし、収差論を構築しただけでなく、実際の設計・製造において奇数次非球面が有効であることを明確に示すことができた。